BASIC-Kurs : "Von Adam und Eva..." (Teil 6)
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
Herzlich Willkommen zum 6. Teil unsers BASIC-Kurses.
Nachdem mich meine Mitredakteure letzen Monat wegen
Platzmangels aus meiner Sparte geschmissen haben,
geht es nun wieder weiter im Text. Allerdings kann
ich Ihnen eine weitere kleine Enttäuschung nicht vor-
enthalten. Ich hatte Ihnen im Mai zwar versprochen,
daß wir uns dieses Mal mit der Grafik beschäftigen
würden, doch möchte ich dies nun erst einmal auf-
schieben. Der Grund hierfür liegt darin, daß nach
diesem Kurs hier ein Grafikkurs geplant ist. Da habe
ich dann auch genügend Platz und Freiheit, Ihnen die-
ses Thema besser zu erläutern und näher zu bringen.
Gerade die Grafik ist beim C64 ein sehr brisantes
Thema, zumal BASIC die Grafikprogrammierung in kein-
ster Weise unterstützt, wie man das von größeren Com-
putern (ich sage da ja nur "AMIGA" und "AmigaBasic")
gewohnt ist. Doch ganau das wird dann Thema dieses
Kurses werden, weshalb ich Sie jetzt noch 3 Monate
vertrösten muß. Dann wird nämlich der Basickurs been-
det sein.
Nun wollen wir aber einmal mit diesem sechsten Basic-
kurs beginnen. Ich möchte Sie nun ein wenig in die
Soundprogrammierung des 64ers einführen, die auch
nicht gerade ohne ist, und für die Sie die Informa-
tionen über das Binärsystem und den Speicheraufbau
des C64 vom letzten Mal genauso, wenn nicht sogar
noch mehr, benötigen.
Erinnern wir uns : mit der Soundprogrammierung hat
der SID, der Chip der Musik erzeugt, etwas zu tun.
Wir hatten ja gelernt, daß die Adressen mit denen man
ihn programmiert im sogenannten I/O-Bereich (INPUT-
/OUTPUT- oder EIN-/AUSGABE-Bereich) liegen, der sich
von Adresse 53248 bis 57344 erstreckt. "Puh!" werden
Sie sagen, "Das sind ja mehr als 4000 Speicherzel-
len ! Wie soll man sich die denn alle merken !" Doch
keine Angst ich kann Sie beruhigen. Der SID belegt
lediglich 28 davon. Ebenso wie alle anderen Ein-
/Ausgabe-Bausteine (es sind derer insgesamt vier, die
wir hier allerdings, außer dem SID, nicht behandeln
werden), die auch nicht mehr als 50 Bytes in diesem
Riesenbereich belegen. Doch Vorsicht. Sie können hier
zwar die meisten Adressen mit beliebigen Werten be-
schreiben, doch ist es NICHT möglich die nicht be-
nutzten Speicherzellen zu benutzen. Sollten Sie hier
einen Wert hineinschreiben, so wird gar nichts pas-
sieren, da die adressierte Speicherzelle nämlich phy-
sisch, also im Innern Ihres 64ers, gar nicht exi-
stiert. Sie bekommen irgendwelche Werte beim Auslesen
mit PEEK geliefert, und beim Schreiben mit POKE wird
der zu schreibende Wert einfach, wie bei einer ROM-
Speicherzelle, ignoriert.
Doch gehen wir nun einmal zu den Speicherzellen die
wir benutzen DÜRFEN. Die sogenannte Basisadresse des
SID liegt bei Adresse 54272. Dies ist die erste Spei-
cherzelle des SID. Sie ist deshalb so wichtig, weil
wir sie benutzen wollen, um sogenannte "Register"
adressieren zu können. Ein Register ist eine Spei-
cherzelle des SID (oder eines anderen I/O-Bausteins)
die man mit Hilfe der Basisadresse und der Register-
nummer anspricht. Hierzu vielleicht ein Beispiel. Mit
dem Befehl:
POKE SI+24,15
setzt man die Lautstärke der erzeugten Töne auf
"laut". Hierbei steht die Variable SI für die Basisa-
dresse des SID, wir haben ihr also vorher den Wert
54272 zugeordnet ! Das Register 24 des SID ist für
die Lautstärke verantwortlich. Schreibt man hier 0
hinein, so wird der Ton gänzlich abgeschaltet. Mit 15
schalten Sie volle Lautstärke ein. Natürlich können
Sie auch alle Werte zwischen 0 und 15 hier benutzen.
Diese sind dann eben je nach dem mehr, oder weniger
laut.
Nachdem Sie nun hoffentlich über die Bedeutung eines
Registers ausfgeklärt sind, möchte ich erst einmal zu
den Grundlagen übergehen. Wie Sie vielleicht wissen
verfügt Ihr 64er über drei "Stimmen". Das heißt er
kann 3 verschiedene Töne gleichzeitig gerenerieren.
Deshalb gibt man einer Stimme des SID auch den etwas
päßlicheren Namen "Tongenerator". Diese sind aufge-
teilt in Tongenerator 1, 2 und 3. Jeder dieser Gene-
ratoren arbeitet unabhängig von den anderen und kann
eigene Töne erzeugen ohne seine Kollegen damit zu
stören. Sie können jeden einzelnen von Ihnen mit ei-
ner bestimmten "Tonhöhe" und einem bestimmten "Klang"
programmieren. Damit Sie dies ein wenig besser ver-
stehen, schlage ich vor, daß wir einmal einen kleinen
Ausflug in die Physik machen:
Wie Sie vielleicht wissen besteht ein Ton, so wie ihn
das menschliche Ohr hört, aus nichts anderem als ei-
nem extrem schnellen Schwingen der Luft. Auch bekannt
unter dem Namen "Schall". Die Art dieses Tones, warum
sich Töne also voneinander unterscheiden können, wird
von zwei Komponenten bestimmt. Da wäre zum einen die
Wellenform und zum anderen die Frequenz. Die Wellen-
form gibt an, wie die Schwingungen verlaufen. Diese
lassen sich durch eine Grafiklinie darstellen, häufig
sogar durch eine mathematische Funktion. Ein Beispiel
wäre da sie Sinuskurve. Mit ihr lässt sich eine Si-
nuswelle erzeugen. Dies klingt dann etwa wie eine
Oboe. Ein weicher und "perfekter" Klang, da die Wel-
lenform ja dem perfektesten geometrischen 2-
dimensionalen Körper zugrunde liegt, dem Kreis.
Jedem der 3 Tongeneratoren Ihres C64 können Sie nun
eine eigene Wellenform einprogrammieren, die dann von
diesem erzeugt wird. Eine Sinuskurve kriegt der SID
zwar nicht ganz hin, doch reicht es immerhin zu einer
Dreieckskurve, die der Sinuskurve in Punkto Hoch- und
Tiefpunkten ja schon sehr ähnlich kommt. Sollten Sie
jetzt hier nur "Bahnhof, Abfahrt und Koffer geklaut"
verstehen, so möchte ich sie mit dem Folgenden
noch ein wenig mehr aufklären. Jede Wellenform kann
nämlich auch mit Hilfe eines Oszillators als Tonwelle
sichtbar gemacht werden. Aus der Schule kennen Sie
bestimmt noch diese Experimente, wo dann auf so einem
kleinen runden Bildschirm eine merkwürdige Kurve er-
schien, wenn der Lehrer irgend einen Ton von sich gab
(oder mit Hilfe eines Tongenerators erzeugte).
Der C64 versteht es nun, 4 veschiedene solcher Kurven
zu erzeugen, zwischen denen Sie dann auch wählen kön-
nen, wenn Sie einem Tongenerator eine "persönliche"
Note geben möchten. Diese sind die Dreieck- (ich hat-
te diese Kurve oben schon erwähnt), Rechteck-, und
Sägezahnkurve. Dann gibt es da noch eine Wellenform
die eher eine Sonderstellung einnimmt, die Rauschkur-
ve. Man kann hier eigentlich nicht mehr von einer
Wellenform reden, da das Rauschen nicht nach einer
vorgegebenen Kurve erzeugt wird, sonden von verschie-
denen Zufallswerten, die den Abstand zum 0-Wert ange-
ben und einfach nur aneinandergereiht werden. So
entsteht ein Eindruck des Rauschens.
Die Rechteckskurve nimmt ebenfalls eine Sonderstel-
lung ein, was ihre Programmierung betrifft. Dies wer-
de ich ein weinig später erläutern.
Wie man nun dem SID klarmacht, welche der 4 Möglich-
keiten man auf einer Stimme spielen möchte, werde ich
Ihnen gleich erklären. Zunächst einmal noch zu der
2ten Komponente, mit der sie einen Ton beeinflussen
können, der Frequenz. Davon haben Sie sicher auch
schon einmal gehört. Je höher die Frequenz ist, desto
schneller wird die Luft zu Schwingungen angeregt. Es
kommen quasi mehr Dreiecksspitzen einer Dreieckkurve
(beispielsweise) in gleichen Zeitabständen an Ihrem
Ohr an, als bei einer niedrigeren Frequenz. Dadurch
werden die Hörnerven mehr gereizt und es entsteht im
Gehirn der Eindruck eines höheren Tones. Dies kann
bis zum Schmerz gehen, wenn der Ton besonders laut
und intensiv gespielt wird, wie etwa bei einer Säge-
zahnkurve, oder bei manchen Rechteckkurven (mit laut
meine ich RICHTIG laut - wenn Sie auf einem Rockkon-
zert einmal nahe den Boxen standen als der Leadgitta-
rist ein Solo von sich gab, dann wissen Sie was ich
meine).
Diese Frequenzen kann man nun auch jedem Tongenerator
angeben, so daß dieser dann genau weiß, wie er den
Ton zu gestalten hat. Um beispielsweise den Kammerton
A zu spielen benötigen Sie eine Frequenz von 440 Hz
(Hertz). Geben Sie diese dem Computer an, so wird er
Ihnen genau diesen Ton vordüdeln. Das hört sich doch
ganz einfach an ! Nun ja, ist es allerdings nicht
unbedingt. Denn Sie können dem SID nicht einfach die
Zahl 440 irgendwo hinschreiben. Dem stehen 2 Dinge im
Weg. Erstens einmal benötigt der SID auch noch weite-
re Angaben über einen Ton, bevor er richtig "losle-
gen" kann und zweitens gibt es mit der Frequenzangabe
auch noch einige kleine Probleme, die etwas mit der
Hardware des 64ers zu tun haben.
Zunächst möchte ich Ihnen eine Übersicht aller SID-
Register geben. Anschließend können wir dann richtig
anfangen. Ich muß noch hinzufügen, daß ich die Regi-
ster 25-28 aus Platzgründen ausgelassen habe. Wir
werden uns mit diesen sowieso nicht befassen, da de-
ren Funktion für uns kaum von Nutzen ist. Nur als
Assemblerroutinen wären diese Register effektiv von
Nutzen, und dann auch nur sehr, sehr selten. Nun aber
zu unsrer Tabelle :
Register Adresse Funktion
–––––––––––––––––––––––––––––––––––––––––––––––––––––
00 54272 Frequenz für Stimme 1 - LO
01 54273 Frequenz für Stimme 1 - HI
02 54274 Pulsbreite für Stimme 1 - LO
03 54275 Pulsbreite für Stimme 1 - HI
04 54276 Ton anschlagen und Wellenform für
Stimme 1
05 54277 Hüllkurve ATTACK/DECAY Stimme 1
06 54278 Hüllkurve SUSTAIN/RELEASE Stimme 1
07 54279 Frequenz für Stimme 2 - LO
08 54280 Frequenz für Stimme 2 - HI
09 54281 Pulsbreite für Stimme 2 - LO
10 54282 Pulsbreite für Stimme 2 - HI
11 54283 Ton anschlagen und Wellenform für
Stimme 2
12 54284 Hüllkurve ATTACK/DECAY Stimme 2
13 54285 Hüllkurve SUSTAIN/RELEASE Stimme 2
14 54286 Frequenz für Stimme 3 - LO
15 54287 Frequenz für Stimme 3 - HI
16 54288 Pulsbreite für Stimme 3 - LO
17 54289 Pulsbreite für Stimme 3 - HI
Register Adresse Funktion
–––––––––––––––––––––––––––––––––––––––––––––––––––––
18 54290 Ton anschlagen und Wellenform für
Stimme 3
19 54291 Hüllkurve ATTACK/DECAY Stimme 3
20 54292 Hüllkurve SUSTAIN/RELEASE Stimme 3
21 54293 Filter-Grenzfrequenz LO
22 54294 Filter-Grenzfrequenz HI
23 54295 Resonanz und Filterschalter
24 54296 Filtermodus und Lautstärke
Doch nun frisch ans Werk. Wie Sie ja gesehen haben
gibt es hier jeweils 7 Register für jede Stimme. Als
aufmerksamer Leser sind Ihnen hierbei bestimmt für
Stimme 1 die Register 00, 01 und 04 aufgefallen. Mit
diesen Registern nämlich können wir unsere Töne
beeinflussen, so wie wir das bisher gelernt haben. In
Register 00 und 01 wird die Frequenz des Tons für
Stimme 1 angegeben und in Register 04 die Wellenform.
Wollen wir nun das Problem lösen, wie wir eine Fre-
quenz, in Hertz gemessen, in diese beiden Register
eingeben. Ich hatte ja schon angedeutet, daß dies
nicht so einfach sein wird.
Ich hole hierzu einmal ein wenig weiter aus. Viel-
leicht haben Sie ja schon einmal gehört, daß der C64
mit einer bestimmten Taktfequenz "getaktet" ist, so
wie das bei jedem Computer der Fall ist. Ein Mikro-
prozesor und überhaupt alle logischen Bausteine in
einem Computer brauchen so etwas ganz einfach, damit
die Arbeiten im Computer geregelt und gleichmäßig
ablaufen. Als Herzstück dient hierzu ein Quarzbau-
stein, der eine bestimmte Taktfrequenz vorgibt. Alle
Bausteine greifen sich nun den Takt von diesem Quarz
ab und modulieren ihn meistens auf eine eigene Fre-
quenz, mit der sie besser arbeiten können. Der Mikro-
prozessor in Ihrem C64 arbeitet zum Beispiel mit ei-
ner Taktfrequenz von 985.2484 KHz. Dies ist genau der
18 Teil der Systemtaktfrequenz, die vom Quarz
herrührt. Diese beträgt demnach 17 734 472 Hz. Also
knapp 17.7 MHz. Der SID benutzt nun ebenfalls diese
Frequenz. Um nun aus internen Gründen des Aufbaus des
SID auf den richtigen Wert zu kommen, mit dem dieser
dann die echte Tonfrequenz spielt muß man vorher noch
eine kleine Umrechnung vornehmen. Diese folgt der
folgenden Formel :
WERT=Tonfrequenz * 2'24 / Taktfrequenz
Möchten Sie also den Kammerton A, mit 440 Hz, spie-
len, so müssen Sie erst den SID-Wert hierfür berech-
nen. Dies sieht dann so aus :
440Hz * 2'24 / 17734472 = 416.25
Lassen wir nun noch die Stellen hinter dem Komma weg-
fallen, so erhalten wir den Wert 416. Genau diesen
Wert müssen Sie jetzt an den SID übergeben, damit
dieser einen 440 Hz-Ton erzeugt. Hierbei haben wir
allerdings ebenfalls noch ein kleines Problem zu
bewältigen. Wie Sie sich errinnern können wir mit dem
POKE-Befehl lediglich ein Byte verändern, also 8 Bit.
Die größte Zahl, die Sie mit dem POKE-Befehl also
übergeben können ist die Zahl 255 (2↑8 Bits - 1), die
nun folgende Zahl, die 256 also, hat jetzt schon 9
Bits, da ja ein Überlauf stattfand. Ich zeige Ihnen
das einmal in Form von (16 stelligen) Binärzahlen:
dezimal binär
255 0000 0000 1111 1111
256 0000 0001 0000 0000
Nun ist aber die Zahl 416 größer als 255, somit müs-
sen wir zu einem kleinen Trick greifen um sie zu
übermitteln. Wir schreiben sie einfach mit 16 Bit, da
eine 16-Bit-Zahl maximal den Wert 65535 aufnehmen
kann, was für unsere Zwecke vollkommen reicht. Dies
sieht dann so aus:
416 (dez.) = 0000 0001 1010 0000 (bin.)
Diese 16-Bit spalten wir jetzt ganz einfach in zwei
8-Bit-Zahlen auf. Die Eine nennen wir "höherwertiges
Byte", die Andere "niederwertiges Byte" einer 16-
Bit-Zahl. Das sähe dann für 416 etwa folgendermaßen
aus :
416 = 0000 0001 1010 0000
Höherwertiges Byte (die ersten 8 Bits von links) :
0000 0001 = 256 (dez.)
Niederwertiges Byte (die nächsten 8 Bits von links) :
1010 0000 = 160
Und siehe da, schon hätten wir unsere Zahl in zwei
Bytes zerlegt, die wir nun einzeln, mit Hilfe des
POKE-Befehls, an den SID übergeben können. Dieser
setzt sie dann intern wieder zusammen und erzeugt
dann die Frequenz 440 Hz !
Für diese beiden Frequenzbytes der Stimme 1 sind nun
die Register 00 und 01 zuständig. Oben in der Regi-
stertabelle waren deren Funktionen beschrieben mit
"Frequenz für Stimme 1 - LO" und "Frequenz für Stimme
1 - HI". Das "LO" und "HI" steht hierbei für "LOw
significant byte" und für "HIgh significant byte"
oder höher- und niederwertiges Byte. Sie müssen also
den LO-Wert von 416, also 160, in Register 00 POKEn
und den HI-Wert 1 in Register 01. Dies sieht als
kleines Programm geschreiben dann so aus :
10 SI=54272:REM BASISADRESSE SID
20 POKE SI+0,160
30 POKE SI+1,1
Und schon wäre der Kammerton A programmiert. Um das-
selbe bei Stimme 2 tun zu können, müssen Sie die Re-
gister 07 und 08 benutzen, bei Stimme 3 Register 14
und 15.
So, die Frequenz wäre gesetzt, aber hören können Sie
jetzt noch nichts. Wir müssen zuerst ja noch die Wel-
lenform angeben. Nehmen wir hierzu doch einfach ein-
mal eine Dreieckskurve. Was ist nun zu tun, um dies
dem SID klarzumachen ? Hierzu benötigen wir für Stim-
me 1 das Register 04 (analog für Stimme 2 und 3, die
Register 11 und 18). Dieses Register vereint mehrere
Funktionen in einem. Die einzelnen Bits in diesem
Register haben verschiedene Aufgaben, die erfüllt
werden, wenn man das entspechende Bit auf 1 setzt.
Ich möchte Ihnen die Bitbelegung hier einmal anhand
einer Grafik darstellen :
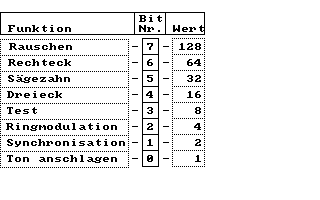
Die Bits 1, 2 und 3 sind für uns unwichtig. Sie akti-
vieren zu komplexe Funktionen, als daß sie hier in
den Kurs passen würden. Für uns sind eher die Bits
4-7 und Bit 0 wichtig. Wie Sie sehen steht jedes die-
ser Bits (außer dem 0.) für eine bestimmte Wellen-
form. Wir möchten nun eine Dreieckskurve spielen.
Also setzen wir einfach Bit 4. Die anderen bleiben
unberührt und haben somit den Wert 0. Unser Byte sähe
Binär geschrieben dann so aus :
0001 0000
Das enstpricht der dezimalen Zahl 16 (der Wert des 4.
Bits). Sollten Sie diese Zahl jetzt in Register 04
schreiben, so wird allerdings immer noch nichts zu
hören sein. Der SID benötigt nämlich noch 2 weitere
Angaben. Zum Einen müssen wir noch die Lautstärke der
vom SID gespielten Musik setzen und zum anderen
braucht dieser auch noch eine sogenannte "Hüllkurve",
die etwas über den Verlauf des gespielten Tons an-
gibt. Kommen wir jedoch erst einmal zur Lautstärke.
Diese schalten Sie am besten auf volle Lautstärke.
Wir hatten dies ja oben schon einmal. Sie müssen ein-
fach den Wert 15 (Maximalwert) in das Lautstärkeregi-
ster 24 schreiben. Also :
POKE SI+24,15
So. Nun machen wir uns einmal an die Hüllkurve heran.
Physikalisch haben wir den Ton ja nun schon festge-
legt. Wir können jetzt allerdings noch seinen
Lautstärkeverlauf, WÄHREND er gespielt wird bestim-
men, eben mit Hilfe der oben genannten Hüllkurve.
Diese besteht aus 4 Phasen. Diese heißen "Attack-",
"Decay-", Sustain-" und "Releasephase" und werden in
der eben angezeigten Reihenfolge vom SID durchgegan-
gen. Wozu nun das ganze ?
Wie Sie ja vielleicht wissen ist nicht jeder Ton, der
die gleiche Frequenz hat, allerdings von 2 verschie-
denen Instrumenten gespielt wird, vom Klang her
gleich. Eine Oboe zum Beispiel hört sich "weicher" an
als ein Glockenspiel, obwohl die Wellenformen einan-
der sehr ähnlich sind. Das Glockenspiel wird "härter"
gespielt als die Oboe. Das heißt, daß beim Anschlagen
einer Metalleiste des Glockenspiels der Ton die mei-
sten Schwingungen erzeugt und somit am lautesten
klingt. Im Gegensatz zur Oboe, bei der die hindurch-
geblasene Luft erst einmal einen Ton erzeugen und
quasi "in Schwingung" gebracht werden muß. Ein ande-
res Beispiel wäre eine Klaviersaite. Schlagen Sie
eine Taste auf der Klaviatur an, so wird der Ton an-
fangs am lautesten sein und nach und nach abklingen.
Dies kann manchmal bis zu 50 Sekunden dauern, wobei
die Oboe kaum mehr als 0.5 Sekunden braucht. Sie se-
hen also, daß ein Ton einen sogenannten Lautstärke-
verlauf bestitzt. Genau diesen Verlauf beschreibt
eben die Hüllkurve. Wie Sie in der obigen SID-Tabelle
sahen sind die Hüllkurvenregister für den ersten Ton-
generator die Register 05 und 06. In ihnen werden die
Werte für die 4 Hüllkurvenphasen gespeichert. Da wir
4 Werte haben, allerdings nur 2 Register, wird dies
so gehandhabt, daß jedes Register in zwei 4-Bit-
Bereiche aufgeteilt wird. So, daß die vier "höherwer-
tigen" Bits eine, und die vier "niederwertigen" Bits
eine andere Phase darstellen. Diese sind folgenderma-
ßen verteilt :
Register Bits 4-7 (HI) Bits 0-3 (LO)
––––––––––––––––––––––––––––––––––––––––
05 Attack Decay
06 Sustain Release
Somit sind Werte von 0-15 für jede Phase möglich
(2↑4-1). Wollen wir nun klären, welche Aufgaben die
einzelnen Phasen haben :
1.) Die Attackphase:
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
Mit ihr kann die Zeit angegeben werden, in der ein
Ton von Lautstärke 0 auf die in Register 24 angegebe-
ne Lautstärke ansteigt, wobei bei dem Wert 0 diese am
schnellsten, und beim Wert 15 am langsamsten erreicht
wird. Hier eine Tabelle mit den genauen Werten :
WERT ZEIT (in Sekunden)
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
0 0.002
1 0.008
2 0.016
3 0.024
4 0.038
5 0.056
6 0.068
7 0.080
8 0.100
9 0.250
10 0.500
11 0.800
12 1.000
13 3.000
14 5.000
15 8.000
2.) Die Decayphase :
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
Diese Phase gibt an, in welcher Zeit der soeben in
der Attackphase erreichte Wert der Lautstärke, auf
den Lautstärkewert absinkt, der als Sustainwert ange-
geben wird.
3.) Sustain-spanne :
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
Hier wird ein Wert zwischen 0 und 15 angegeben, der
die Endlautstärke nach ablauf der Decay-Phase angibt.
4.) Releasephase :
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
Wird ein Ton abgeschaltet (dazu kommen wir gleich
noch) dann wird unverzüglich die Releasephase einge-
leitet. Sie gibt an in welcher Zeit der Ton von der
Sustainlautstärke wieder auf 0 absinkt.
Die Zeitwerte für die Decay- und Releasephase können
Sie der folgenden Tabelle entnehmen :
WERT ZEIT (in Sekunden)
‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾‾
0 0.008
1 0.024
2 0.048
3 0.072
4 0.114
5 0.168
6 0.204
7 0.240
8 0.300
9 0.750
10 1.500
11 2.400
12 3.000
13 9.000
14 15.000
15 24.000
Angenommen, wir wollten ein Glockenspiel mit dem SID
simulieren, dann bräuchten wir einen Ton der schnell
auf voller Lautstärke steht und dann auch relativ
schnell wieder abklingt. Wählen wir also folgende
Werte für die einzelnen Phasen :
Attack - 00
Decay - 07
Sustain - 09
Release - 01
Die 2 Bytes für die Hüllkuve müßten dann folgenderma-
ßen aussehen :
1.) 0000 0111
A=0 S=7
2.) 1001 0001
S=9 R=1
Nun müssen Sie diese Bytes also nur noch ins dezimale
System umrechnen und in die Register 05 und 06 poken.
Die Werte wären demnach 7 und 145. Zugegebenermaßen
ist dies eine ein wenig mühselige Arbeit, wenn man
nicht gerade über einen Taschenrechner verfügt, der
das Binärsystem beherrscht. Deshalb kann das auch ein
wenig einfacher gehandhabt werden. Denn ebenso, wie
man HI- und LO-Bytes bilden kann, lassen sich auch
"HI- und LO-Halb-Bytes" bilden. Diese heißen dann
"Nibble". Nun müssen Sie nur noch nach einem bestimm-
ten Schema die verschiedenen Werte miteinander zu
multiplizieren (der Umgekehrte Weg der Zerlegung in
LO- und HI-Byte). Nämlich nach der Formel :
HI-Nibble * 16 + LO-Nibble
In unserem Fall hätten wir dann folgende Berechnungen
durchzuführen :
Attack- und Decay-Byte : 0*16+7= 7
Sustain- und Release-Byte : 9*16+1=145
Und schon wären wir am Ziel. Nun gilt es nur noch die
Werte im SID zu setzen, also :
POKE SI+5,7
POKE SI+6,145
Das wäre geschafft ! Doch - oh Enttäuschung - es
kommt immer noch nichts aus dem Lautsprecher !!! Kei-
ne Panik, das ist ganz normal so, denn wir haben noch
eine weitere Operation durchzuführen. Der SID weiß
jetzt zwar welche Frequenz er zu spielen hat, was für
eine Wellenform er unserem Ton geben soll, und wel-
chen Klangverlauf dieser haben soll, damit er aber
nun endlich die Hüllkurve abspielt, muß man ihm auch
noch mitteilen, wann er dies zu tun hat. Wir müssen
ihm also quasi ein "Startzeichen" geben, daß er die
Attackphase einleiten darf. Dies geschieht mit Hilfe
des 0. Bits aus Register 04 (ich hatte es vorhin
schon einmal erwähnt, siehe auch Grafik). Erst wenn
dieses Bit gesetzt wird, beginnt er nämlich die At-
tackphase einzuleiten. Wir müssen somit also zu dem
Wellenform-Wert 16 für die Dreieckskurve auch noch
eine 1 addieren, damit dies der Fall ist (1 ist die
Wertigkeit des 0. Bits). Schreiben Sie also nun fol-
genden Befehl :
POKE SI+4,17
Nun kommt er endlich aus dem Lautsprecher, unser lang
erwarteter Ton. Lange hat es gedauert, doch schließ-
lich und endlich haben wir es doch noch geschafft!
Wie Sie jetzt allerdings schnell merken werden, hört
er gar nicht mehr auf zu spielen, sondern brummt mun-
ter weiter. Das war allerdings gar nicht der Effekt,
den wir erzielen wollten. Der Ton sollte doch eigent-
lich wieder in der Releasephase abklingen ! Der Grund
hierfür liegt darin, daß die Releasephase noch gar
nicht eingeleitet wurde ! Dies geschieht nämlich
erst, wenn das 0. Bit in Register 04 wieder auf 0
gesetzt wird. Bitte, probieren Sie - diesmal kommt
also nur 16 in dieses Register, da wir ja die
Dreieckswellenform ja noch beibehalten möchten, al-
so :
POKE SI+4,16
Und schon hört der Krach auf. Dies ist ein Punkt den
Sie beim Soundprogrammieren genauestens beachten
sollten. Die Zeit, in der der Ton auf der Sustain-
Lautstärke gehalten wird, bestimmen Sie als Program-
mierer, nicht der SID. Sie müssen ihn erst "von Hand"
wieder abschalten. Praktisch läßt sich das etwa mit
einer Verzögerungsschleife realisieren.
Sie programmieren einfach eine Schleife, in der der
Computer zwar mit dem Abarbeiten der Schleife
beschäftigt ist, jedoch nichts tut. Es fehlt ganz
einfach der Schleifenrumpf. Hier ein Beispiel :
FOR I=1 TO 100:NEXT
Sie sehen, die Schleife zählt ganz still und heimlich
bis 100. Effektiv tut der Computer jedoch nichts. So
können wir das Programm mit Scheinberechnungen quasi
"anhalten", damit der SID auch genug Zeit hat, die
ersten 3 Phasen auch durchzuspielen. Am besten sehen
Sie sich einmal das Programm "MINISOUNDDEMO" auf der
Rückseite der MagicDisk einmal an. Hier habe ich alle
notwendigen Befehle noch einmal zusammengerafft,
damit Sie auch ein kleines praktisches Beispiel ha-
ben.
Nun will ich Ihnen noch erklären welch eine Besonder-
heit die Rechteckskurve auf sich hat, und wofür die
Register 02 und 03 benutzt werden. In diesen beiden
Registern können Sie nämlich die Pulsbreite der Rech-
teckskurve für Stimme 1 angeben. Wie Sie oben in der
Wellenformgrafik gesehen haben, wird der Abstand, der
zwischen den beiden Punkten liegt, an dem die Recht-
eckskurve von ihrem Tiefstpunkt zu ihrem Höchstpunkt
"springt" in der sogenannten "Pulsbreite" angegeben.
Sie können in diesen beiden Registern also ganz ein-
fach den Abstand dieser beiden Rechtecksseiten ange-
ben. Dadurch können Sie den Klang der Rechteckskurve
noch einmal drastisch verändern. Mit niedrigen Puls-
breiten gespielt hört sich diese Welle sehr "kräch-
zend" an, fast schon wie ein "Sägezahn". Je größer
die Abstände werden, desto weicher und voller wird
der Klang. Hier liegt es an Ihnen, die einzelnen
Zustände einmal durchzuprobieren. Es sei nur noch
gesagt, daß hier mit einem 12-Bit-Wert gearbeitet
wird. Das heißt, daß die Bits 4-7 von Register 03
KEINE Auswirkung auf die Pulsbreite haben. Der maxi-
male Pulsbreitenwert liegt somit bei 2↑12-1, also
4095. Probieren Sie einfach einmal ein wenig herum,
denn, wie heißt es so schön : "Nur die Übung macht
den Meister." Wie Sie dies handhaben, sollten Sie ja
mittlerweile wissen, ich hatte Ihnen die Problematik
von HI- LO-Byte oben ja schon erklärt. Sie müssen
hier nur darauf achten, daß Sie im Register 04 auch
die Rechteckwellenform einschalten, und daß das HI-
Nibble (Bits 4-7) der Pulsbreite immer 0 ist.
Im übrigen sei noch erwähnt, daß Sie alle hier ge-
nannten Vorgänge mit Registern usw. natürlich eben-
falls an den Stimmen 2 und 3 durchführen können. Sie
müssen nur in der Registertabelle nach dem entspe-
chenden Äquivalent des Registers für die entspechende
Stimme suchen. Sie werden merken, daß diese alle in
der gleichen Reihenfolge für die einzelnen Stimmen
angeordnet sind. Im übrigen sind die meisten Register
des SID nicht auslesbar (bis auf die der 3. Stimme).
Es passiert also dasselbe, wie wenn Sie auf eine der
oben erwähnten I/O-Adressen zugreifen...
Ich möchte mich nun bis nächsten Monat wieder verab-
schieden, wenn wir uns dann ein wenig mit der Daten-
speicherung und der Peripherie des 64ers beschäftigen
werden. Sie werden dann auch gleich noch den noch
fehlenden Befehlssatz von BASIC 2.0 kennenlernen.
Ich bedanke mich nun für Ihre Aufmerksamkeit und wün-
sche ein fröhliches SID-Gedüdels, bis in einem Monat,
Ihr Uli Basters.
