Teil 4 Grafikkurs
----------------------------------------
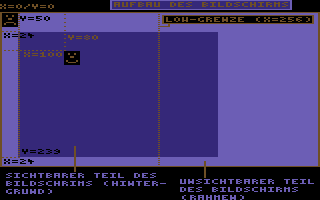
Wie Sie erkennen können, liegt unser
Sprite (wenn es die Koordinaten 0/0 hat)
ganz genau in der linken oberen Ecke des
Bildschirms, allerdings im unsichtbaren
Breich. Erst ab den Koordinaten X=24 und
Y=50 beginnt der sichtbare Bildschirmbe-
reich. Da sich unser Sprite in einem
Koordinatenbereich befindet der kleiner
als die ersten sichtbaren Koordinaten
ist, kann man es natürlich noch nicht
sehen. Wozu dies alles gut sein kann,
werden wir später noch sehen.
Zunächst einmal wollen wir unser Sprite
einmal auf den Bildschirm bringen. Hier-
zu müssen wir lediglich die entsprechen-
den Bildkoordinaten in die Koordinaten-
register unseres Sprites schreiben. Das
sind für Sprite 0 die Register 0 und 1
für die X- und Y-Koordinate. Positionie-
ren wir unser Sprite doch einfach einmal
in der Ecke links oben, diesmal jedoch
die Sichtbare :
POKE V+0,24 :REM X-KOORDINATE
POKE V+1,50 :REM Y-KOORDINATE
So. Nun müßten Sie endlich unser Sprite
auf dem Bildschirm sehen. Da steht es
nun und läßt sich durch nichts beein-
drucken. Lassen Sie doch einmal den
Bildschirm nach oben scrollen, indem Sie
mit dem Cursor in die untere linke Ecke
fahren und eventuell vorhandenen Text
"nach oben rollen" lassen. Sie werden
bemerken, daß unser Sprite kontinuier-
lich auf seiner Stelle stehen bleibt und
sich nicht von seiner links-oben-
Position wegbewegen läßt. Sprites sind
somit also tatsächlich unabhängige Gra-
fikobjekte, mit denen man ganz eigene
Dinge machen kann.
Nun, man muß zugeben, daß ein unbewegli-
ches Sprite auf die Dauer ziemlich lang-
weilig werden kann. Wie wäre es denn,
wenn wir unseren kleinen Freund zuerst
einmal aus dem oberen Bildschirmrand
runterlaufen ließen, und ihm dann einen
Richtungswechsel nach rechts verpaßten ?
Nichts einfacher als das ! Hierzu müssen
wir einfach eine Schleife schreiben, die
die X-, beziehungsweise Y-Position unse-
res Sprites erhöht, oder erniedrigt.
Hier ein Beispiel (wir setzen voraus,
daß alle Daten schon im Speicher stehen,
und das Sprite ordungsgemäß eingeschal-
tet wurde) :
10 v=53248
20 POKE V+0,24 :REM SICHTBARE
X-KOORDINATE.
30 FOR I=39 TO 150 :REM VON 39 BIS 150
ZÄHLEN...
40 FOR K=0 TO 10:NEXT K
:REM VERZöGE-
RUNGSSCHLEIFE, SONST
GEHTS ZU SCHNELL
50 POKE V+1,I :REM Y-POS SETZEN
60 NEXT I
70 :
80 FOR I=24 TO 255 :REM JETZT VON 24 BIS
255 ZÄHLEN...
90 FOR K=0 TO 10:NEXT K:
:REM WIEDER VERZöGE-
RUNG, DAMITS FÖRS
AUGE SICHTBAR WIRD.
100 POKE V+0,I
110 NEXT I
Wenn Ihnen das hier zu unübersichtlich
ist, dann starten Sie doch einfach ein-
mal das Programm "MOVESPRITE" auf der
Rückseite der Magic Disk. Hieran sehen
Sie dann auch wozu so ein "unsichtbarer"
Bildschirmbereich nützlich ist. Man kann
nämlich ein Sprite kurzerhand in den
sichtbaren Bereich hineinbewegen, daß
ist bestimmt ein besserer Auftritt für
unseren kleinen Freund, als wenn er ein-
fach - Zack - auf dem Bildschirm er-
scheinen würde...
Vielleicht ist Ihnen in diesem Beispiel
hier ja aufgefallen, daß ich die X-
Koordinate nur bis 255 gezählt habe, und
wenn das nicht der Fall war, dann hat
Sie aber ganz sicher der Ausdruck "Low-
Grenze" in der letzten Grafik stutzig
gemacht. 255 ist ja der höchste Wert den
ein Byte annehmen kann. Für die X-
Koordinate ist dies also der größtmö-
glichste einsetzbare Wert. Wenn Sie
jetzt einmal ein Sprite an die X-
Position 255 setzen, dann werden Sie
sehen, daß es noch mitten auf dem Bild-
schirm steht. Was aber, wenn wir den
Bereich ab 255 noch nutzen, unser Sprite
also noch ein bisschen weiter bewegen
möchten ? Hierfür ist, wie Sie es in der
Liste der VIC-Register vielleicht schon
gesehen haben, Register Nummer 16 ver-
antwortlich. Das Hauptproblem, das wir
nämlich haben, ist, daß das X-Register
eines Sprites nur auf 8 Bit begrenzt
ist. In Register 16 stellt uns der VIC
nun ein weiteres, neuntes Bit zur Verfü-
gung. Das Register 16 selbst hat ja
ebenfalls 8 Bits, für jedes Sprite eins.
Für Sprite 0 ist Bit 0 zuständig, für
Sprite 1 gibt es das Bit Nummer 1 und so
weiter...
Doch wozu brauchen wir die ganzen neun-
ten Bits ? Ganz einfach, dadurch erhöht
sich der Wertebereich des Ganzen nämlich
auf (dezimal) 512 X-Positionen (die 0.
Position miteingerechnet) ! Sie müssen
sich also für die X-Position eine 9-
Bit-Binärzahl vorstellen. Wollenten wir
unser Sprite beispielsweise an Position
256 setzen, so wäre die 9-Bit-
Kombination "1 0000 0000" - das neute
Bit wäre also gesetzt, alle acht anderen
gelöscht. Die ersten acht Bits kommen
immer in das "normale" X-Register eines
Sprites. Das neunte nun schreiben wir in
Register 16. Bei Sprite 0 wäre das ja
das 0. Bit dieses Registers. Dieses hat
den Dezimalwert 1, also schreiben wir in
V+16 den Wert 1 und schon hätten wir
unser Sprite ein Stückchen weiter über
die Low-Grenze hinausgeschoben. Also :
POKE V+0,0
POKE V+16,1
Wollten wir es jetzt weiterbewegen, so
müßten wir einfach wieder das X-Register
verändern, das neute Bit in Register 16
ist ja jetzt gesetzt. In unserem Bei-
spielen vorhin, war es - wenn Sie Ihren
64er gerade frisch eingeschaltet hatten
- schon von Haus aus auf 0, deshalb ist
unser Sprite dann auch in der linken
Bildschirmhälfte erschienen. Wird jedoch
das neute Bit der X-Koordinate gesetzt,
dann dient nun als relativer Anfang-
spunkt die Bildschirmposition 256. Ach-
ten Sie also immer darauf, daß Sie beim
Positionieren von Sprites immer eine
9-Bit-Zahl verwenden, wobei das neute
Bit immer in Register 16 wandert und die
restlichen acht im entsprechenden X-
Register des Sprites landen. Setzen wir
doch einfach einmal Sprite 1 an die X-
Koordinate 300. Binär gesehen hat 300
die folgende Kombination :
1 0010 1100
Demnach müssen wir also Bit 1 im Regi-
ster 16 setzen. Dieses hat den Dezimal-
wert 2. Die restlichen 8 Bits haben ins-
gesamt den Dezimalwert 44. Also :
POKE V+16,2 :REM HI-BIT SPRITE 1 SETZEN
POKE V+2,44 :REM X-POSITION SPRITE 1
Sehen Sie Register 16 also bitte als
eigenständiges Register an. Auch hier
müssen 8-Bit Werte hineingeschrieben
werden ! Wollten Sie also beispielsweise
Sprite 0, 2 und 5 in einen X-Bereich
hinter 256 setzen, so müßten Sie den
entsprechenden Dezimalwert, nämlich 37,
ganz normal in dieses Register hinenPO-
KEen !!!
Eine andere Möglichkeit gibt es durch
die logischen Operatoren, die ich im
BASIC-Kurs bewußt NICHT behandelt habe,
da sie wirklich nur eine wichtige Rolle
in der Grafik spielen. Deshalb möchte
ich dies hier noch nachholen.
Die logischen Operatoren kann man wie
die arithmetischen Operatoren (+,-,*,/)
verwenden. BASIC stellt uns ihrer drei
zur Verfügung, nämlich AND, OR und NOT.
Man kann logische Operatoren hervorra-
gend zur gezielten Manipulation von Bits
benutzen, ohne voher irgendwelche Binär-
zahlen in Dezimalzahlen umrechnen zu
müssen und umgekehrt. Bei AND und OR
werden ganz einfach zwei Binärzahlen und
ihre Bits miteinander verglichen, und
nach einer logischen Entscheidungstabel-
le resultiert aus dem Zustand dieser
Bits ein bestimmtes Ergebnis. Das hört
sich vielleicht komplizierter an als es
ist. Beginnen wir doch einfach einmal
mit einem Beispiel. AND ist englisch und
heißt UND. Ich möchte nun einmal ganz
einfach mit dem AND-Operator verglei-
chen, und Ihnen das Ergebnis erklären.
Hier erst einmal das Beispiel :
0100 0010 (dez. 66)
AND 0101 0000 (dez. 80)
-----------------------
= 0100 0000 (dez. 64)
Der Computer hat hier zwei 8-Bit-Zahlen
miteinander geUNDet. Hierbei hat er im-
mer das n-te Bit der ersten Zahl mit dem
n-ten Bit der zweiten Zahl verglichen
und dann ein aus den beiden Bits resul-
tierendes Bit ermittelt. Hierbei ging er
nach dem Schema vor, daß nur, wenn das
Bit der ersten Zahl UND (AND) das Bit
der zweiten Zahl 1 oder 0 war, das re-
sultierende Bit ebenfalls gleich 1 oder
0 war. In allen anderen Fällen, also
wenn das Bit der ersten Zahl gleich 0
und das Bit der zweiten Zahl gleich 1
war (beziehungsweise umgekehrt), war das
resultierende Bit gleich 0 !
Ebenso verhält sich das bei OR, was auf
Deutsch ODER heißt. Hier ein Beispiel :
0100 0010 (dez. 66)
OR 0101 0000 (dez. 80)
-----------------------
= 0001 0010 (dez. 18)
Sie sehen, als Ursprungszahlen habe ich
dieselben genommen wie eben, jedoch ist
das Ergebnis nun ein anderes. Hierbei
waren ja auch die Enscheidungskriterien
nicht dieselben. Das resultierende Bit
aus den zwei n-ten Bits einer Zahl war
nämlich nur dann 1, wenn das Bit der
ersten Zahl ODER (OR) das Bit der zwei-
ten Zahl gesetzt war. ODER wenn beide
Bits gesetzt waren. Nur wenn Beide 0
waren, war das resultierende Bit eben-
falls gleich 0 !